图片:
开始也认为二轴干不成,必须三轴,经分析发现二轴可以完成。下面简单分析下工件转角和滑台的位移关系。
先分析加工正方形。
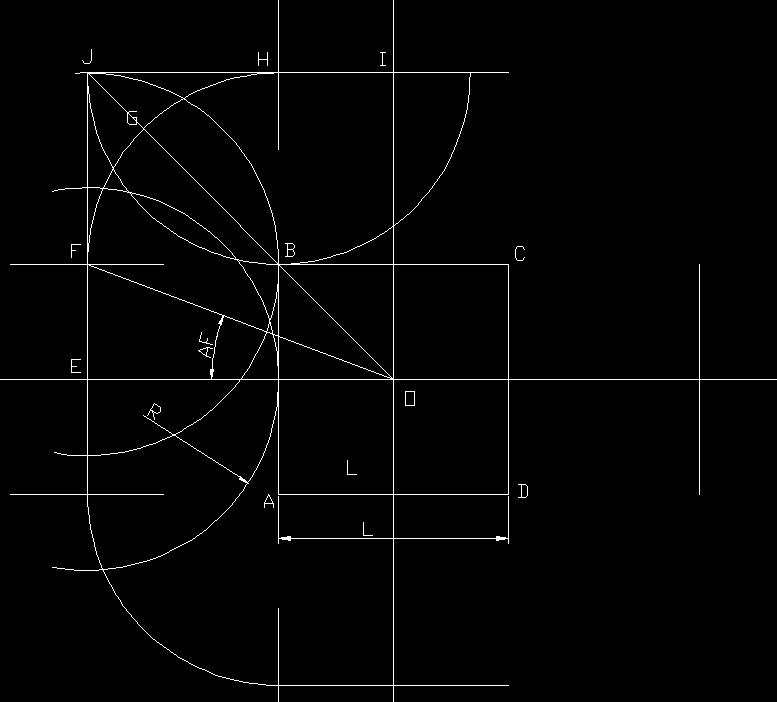
设:正方形ABCD的边长为L,沙轮的半径为R,则沙轮中心到工件中心的基准 OE=R+L/2
加工是工件转动,根据工件的转角滑台作对应的移动。要求解的就是工件转角和滑台的位移关系。
根据运动的相对性,为方便分析,转化成工件不动,沙轮绕工件转动同时沿半径方向移动。因为对称,只要分析四分之一周期。
如图,沙轮中心按 E-F-G-H-I.... 运动,即能切削出正方形。而在(F-G-H)圆弧段对应加工点是B点尖角,基本不切削,可以让沙轮离工件远些,改成走E-F-j-H-I两段直线,计算更方便。
实际只要计算一条边,转角从-90度 到 +90度 (计算要改用弧度计算)
如 转角为 AF,基准距离为 OE=R+L/2,相对于基准距离的滑台位移 S
-PI/4 <= AF <= PI/4 PI=3.141592 (弧度)
工件转角对应的工件与沙轮的中心距 OF
OF=OE/COS(AF)=(R+L/2)/COS(AF)
相对于基准距离的滑台位移 S
S=OF-OE=(R+L/2)/COS(AF)-(R+L/2)=(R+L/2)/(1/COS(AF)-1)
这就是需要的关系公式,我只能提供这些了,其他要你自己解决。
椭圆就更复杂,搞这项目要有数学基础
当然加工时工件转速不能快,这是由磨削加工决定的,所以滑台速度也不会快。